Prime-factorisation
Though a horse that can do arithmetic, undoubtedly qualifies as a talented horse, it's shouldn't automatically qualify as a talented mathematician. Never-the-less, it's either horse-power or a magic quantum-computing bullet, that is currently required to factorise large integers. The largest semi-prime (which doesn't have some special property) which has been factored, has only 232 decimal digits. That might sound like a large integer, & it would be if you were holding a tape-measure round your waistline, but not when the likelihood of maintaining a positive balance in one's internet-accessible bank-account, depends on the difficulty of determining its prime-factors.
Algorithms

- Trial Division:
-
Simple to comprehend & implement. It's best suited to smooth integers; regrettably such integers are the low-hanging fruit, & it has dubious applicability to the unruly remainder (e.g. those used in public-key cryptography).
- Fermat's method:
-
More complicated than by Trial Division, but may be faster when the prime factors happen to be close to the square-root of the original composite integer; but one probably doesn't know that until after the time has been spent finding them. Never-the-less, it is important, because it forms the basis of faster tests (which I haven't implemented yet).
Testing
For test-data, I've used the odd members of the Fibonacci-sequence.
I have chosen not to check for primality first. Though this might avoid wasted effort, & therefore might be an appropriate strategy in a real-world scenario, the characteristics of the prime-factorisation algorithm under test, would be obscured by those of the (arbitrarily chosen) primality-algorithm.
Because of the different suitabilities of the algorithms under test, the performance is going to be very dependent on the specific test-integer, & consequently, one must view the results from a sufficient distance to see the underlying trends over a large number of test-data.
Results
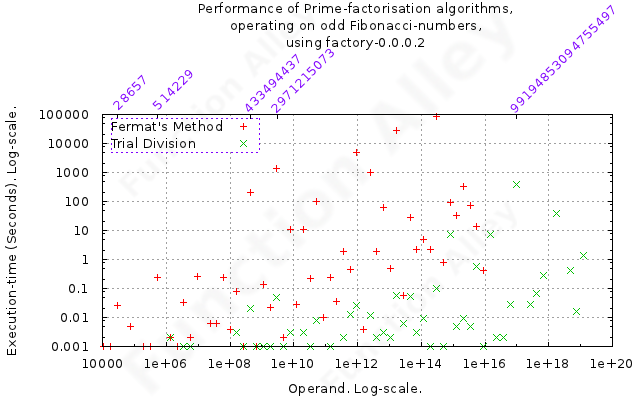
Both algorithms search though a set of potential prime factors looking for matches, & on finding one they can factor the original integer & recurse, but if there are no factors, this fruitless search will be long. So both algorithms can be expected to perform badly when asked to decompose a prime number. Because of the unpredictable distribution of prime-numbers, unpredictable performance-spikes may be expected to cloud the results. The primes within the test-data have been marked on the graph of results. This could have been avoided by preceding prime-factorisation by a rapid primality-test, but for the reasons stated above, this hasn't been done.
The performance using Fermat's Method, was so bad for the semi-prime 14472334024676221, that I terminated the test.
My original implementation of both algorithms below, attempted to memoize the results, by constructing a conceptually infinite, lazy list, of the prime factors of all positive integers, so that after each prime factor was found, recursive invocations on the cofactor, could reuse any prime-factors found in previous calls. This used far too much RAM, & if only the prime-factorisation of small integers are stored, then the time-savings aren't significant. After removing this premature optimisation, neither algorithm made any significant demands on RAM; so I haven't bothered to plot it.
Conclusions
One can conclude that the execution-time generally increases with the magnitude of the operand (no surprises there), but because of the erratic performance, it's not possible to say precisely what that relationship is. As expected, the results are blighted by poor-performance, by either algorithm, when attempting to find the non-existent factors of prime integers, but this is only of significant when the operand is also large.
Both algorithms also suffered from poor performance when attempting to factorise rogue composite integers, in an algorithm-specific way.
- Trial Division:
-
Performed poorly on rough integers.
- Fermat's Method:
-
Performed poorly on integers with prime-factors remote from its square-root; e.g. the integer at which the test was prematurely terminated, has prime factors 157 × 92180471494753, & square-root ≅ 120301014.23.
Within the domain of integers tested, Trial Division, is nearly always better. Beyond this domain, it's arguable that neither algorithm is appropriate, & I should implement a better one.