Primality-tests
A primality-test tells one nothing about the specific prime factors, to which a composite integer can be decomposed, merely whether that integer is prime. This, being potentially cheaper to ascertain, often precedes the more demanding requirement of prime-factorisation.
Algorithms
- The AKS primality-test:
-

The world changed in when the AKS primality-test landed. This, for the first time, provided;
- a deterministic test,
- applicable to all integers,
- executable in polynomial time,
- & independent of unproven assumptions.
Regrettably, there's a fly in the ointment: the degree of that polynomial time-complexity is unfeasibly high. The algorithm has subsequently been tweaked several times to reduce it, but it's still too high for this algorithm to be more than merely a hope of things to come.
- The Miller-Rabin primality-test provides:
-
- a deterministic test (in the form implemented here, though there's also a faster probabilistic version),
- applicable to all integers,
- executable in polynomial time, with a lower degree than AKS.
- but its validity depends on the unproven Generalized Riemann-hypothesis.

Testing
For test-data, I've used the members of the Fibonacci-sequence indexed by a prime-number; which (bizarrely) include all but one of the Fibonacci-primes, along with some composite integers.
Results
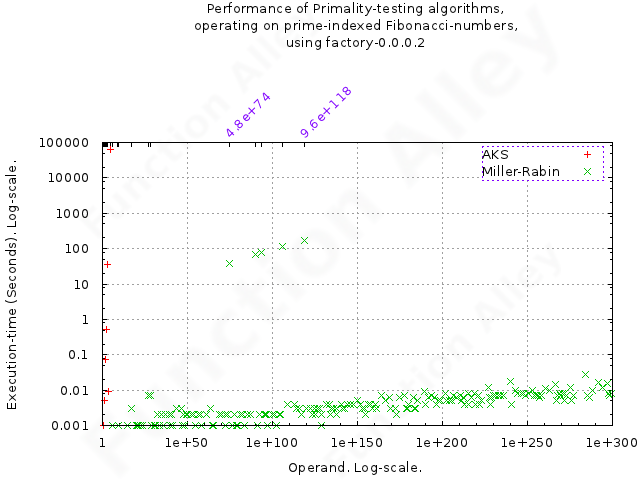
The difference between the two algorithms could not be more pronounced:
-
The AKS algorithm, with all it's theoretical credentials, performs so badly that, within the domain of integers tested, performing complete factorisation would have been faster. I terminated the test after it took 65686s to determine that 28657 was prime (it took Miller-Rabin and Trial Division an unmeasurably small time). Other published implementations of this algorithm have found it to suffer from dismal performance, & have identified the culprit to be polynomial-exponentiation. It does parallelize effectively (though these tests were performed on just one CPU-core), & there's almost certainly scope for improvement within this Haskell-implementation, but it's equally probable that it's never going to be competitive.
-
The implementation of the Miller-Rabin primality-test, performed so quickly that the execution-times rarely emerge from the background noise, & testing was ultimately limited by gnuplot, which couldn't cope with integers exceeding 10300. The execution-time spikes briefly between 4.8×1074 & 9.6×10118, corresponding to Fibonacci-primes, located at prime positions [359, 431, 433, 449, 509, 569, 571] in the sequence. After that, the next Fibonacci-prime, at position 2971 (of approximate value 3.6×10620), lies beyond the test-domain, hence the lack of further spikes in the execution-time.
Neither algorithm made any significant demands on RAM; so I haven't bothered to plot it.
Conclusions
-
Though the AKS performed so badly that it's of no current value, this is a relatively new concept, & has the promise of reductions in time-complexity in the future.
-
The Miller-Rabin primality-test, was sufficiently rapid, for it to be used prior to complete prime-factorisation, to avoid futile attempts to factorise a prime, without concern for the detrimental effect it will then have on performance when it identifies a composite integer.