Prime-number Generation

Algorithms

In each of these algorithms, one draws candidates from a list of increasing integers, starting at the first prime, 2, & sieves them to remove those which are composite, thus leaving only the primes, as required.

Many algorithms in this domain, can be made to work much more efficiently when the list of candidates is finite, i.e. capped by an upper bound, & some can only work given this constraint. Despite the advantage, this constraint has not been enforced in most of the implementations presented here; they typically operate on a list of candidates which lacks any upper bound, & is consequently infinite, liberating the user from the requirement to define in advance, the maximum prime required … which is often unknown.

Trial division:

One rejects candidates divisible by any of the primes previously found. If a candidate is indivisible by all the primes previously found, then it must itself be prime, & is added to the list against which future candidates must be proved. Since the list of known primes inevitably grows, the burden associated with proving the primality of subsequent candidates increases, suggesting an inherently poor time-complexity.

Turner's sieve:

The head of the list of candidates, is always guaranteed to be prime, & is used to filter the infinite list of remaining candidates, removing all those it divides. Dealing with infinite lists in conventional strict languages makes your head hurt, but the default lazy evaluation of Haskell, merely makes you jaw feel rather slack. Haskell code for this algorithm is frequently seen because of the beguilingly terse solution.

primes = 2 : sieve [3, 5 ..] where sieve (p : xs) = p : sieve [x | x <- xs, rem x p /= 0]

Whilst the result seems to spring into existence like the creation of the Infinite Improbability Drive, it's not expected to share the stellar performance, since sadly it has already been unmasked, as Trial Division in disguise.

The Sieve of Eratosthenes:

This algorithm doesn't involve division; just multiplication, which is theoretically cheaper. As each prime is discovered, all its non-trivial multiples (starting from its square), which are by definition composite, are recorded. Each subsequent candidate must either be a member of this set of composites, or a prime, whose multiples are then recorded in the expanding set.

The secret to a successful implementation, lies in the container used to store the set of prime-multiples, which is required to support fast random insertion, fast inspection of the minimum value contained, fast deletion; fast everything really. The functional requirements initially suggest a Set, but since only the smallest unmatched multiple is ever of relevance, a Priority Queue is a closer match; the standard Haskell library lacks one of these, but Hackage provides PQueue. Regrettably, though this functioned as required, it didn't provide as fast a solution as a more complicated arrangement of two separate containers, a Seq supporting fast append & inspection of the head, & Map supporting fast random-access.

The Sieve of Atkin:

This algorithm differs from those previously described, in that it is, by necessity, bounded.

It has a higher theoretical efficiency than the Sieve of Eratosthenes, since whilst they both eliminate from the list of candidates, integral multiples of each prime discovered (starting from its square), the Sieve of Eratosthenes repeatedly attempts to eliminate, those composites which are integral multiples of more than one prime (E.g. 12 = 2² × 3, would be eliminated, as required, after the discovery of the first prime, but also after the discovery of the second). To reduce this redundant effort, it records the union of the sets of solutions, to three bivariate polynomials, whose value matches any of the candidate integers in the specified bounded range. From the subset of candidates for which there are an odd number of solutions, it then only needs to eliminate those which are integral multiples of the square of those primes previously discovered.

OK, that explanation probably left you quite bewildered, since it doesn't attempt to explain why a set of quadratic polynomials has anything to do with primality-testing; but my point is more about the required procedure. The typical implementation in an imperative language, uses a mutable array to record the number of solutions to these polynomials, equaling each candidate integer, & though Haskell supports many types of array, the mutable ones are more awkward to use, & the immutable ones seem insufficiently efficient to realize the algorithm's potential. The solution adopted here, was to merely list the solutions, & the subsequent selection of just those candidates with an odd number of solutions, was facilitated by sorting this list, & measuring the length of spans, of solutions of equal value. This single operation has a time-complexity O(n×log n), & since the length of this list is proportional to the required range of numbers from which primes are sieved, this exceeds that theoretically achievable for the whole algorithm; consequently this implementation can't currently deliver.

30-spoke Wheel representing primes; 2, 3 & 5.

Regardless of the chosen sieve, it isn't necessary to include non-trivial multiples of 2 (i.e. the even integers) in the list of candidates, since they're all clearly composite. This simple measure halves the number of candidates which must subsequently be sieved. One can in principle extend this concept, with diminishing returns, to preclude the non-trivial multiples of any number of primes, but whilst the even numbers are easy to identify, candidates composed from larger primes require more effort. It is effectively the original problem (i.e. how to construct a prime-sieve), but with an important simplification; if the set of primes which we seek to preclude from the subsequent rigorous sieve, is bounded & small, it can be solved more efficiently using the concept of a wheel. It's so called, because one can visualise it as a wheel, with radial spikes protruding from its circumference, at angles around its circumference corresponding to the multiples of those primes one wishes to preclude. Once constructed, it operates without the need for further division or multiplication. On being rolled along a virtual strip of paper, marked at regular intervals, with the increasing sequence of integers starting from 1, the wheel will pierce holes in those which are multiples of any of the subset of primes from which the wheel was composed, allowing one to identify & excluded them, leaving only those few which are coprime to all of the wheel's primes, to be rigorously sieved.

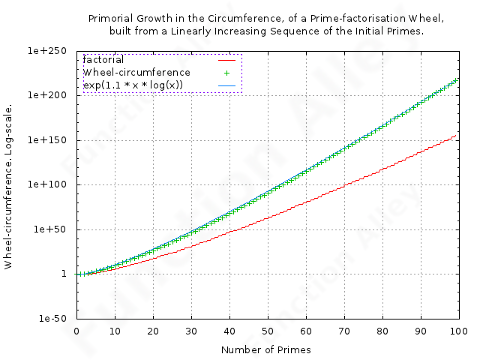
If one decided to preclude the multiples of the first two primes, 2 & 3, then one would use a six-spoke wheel, with spikes at spoke-numbers 2, 3, 4 & 6, which then punches holes at all the multiples of both these primes. Note that the integers left by the 30-spoke wheel depicted are all apparently primes, but this is coincidental, some composite integers will eventually slip through the net (e.g. 49), thus requiring a subsequent rigorous sieve.

The pattern of spikes only starts to repeat, after the circumference exceeds the least common multiple of the set of primes which the wheel represents (& for prime numbers, that equals their product), so the growth in the wheel's circumference is the primorial function. This limits the minimum size of the wheel required to represent all the multiples of a given number of primes. It is the explosive growth-rate in the circumference, which limits the number of primes which can, in practice, be represented by a wheel. The construction of an excessively large wheel, may consume more time than it subsequently saves, & though the exact threshold at which this occurs depends on the number of rotations through which it is subsequently rolled, which in turn depends on the maximum prime demanded, this is rendered moot by the gargantuan space-requirement. One may decide to save space by defining only half the wheel, deriving the other half on demand, by symmetry under reflection, but one would not typically use a wheel composed from more than about the first eight primes.

Results

Memory-requirement for Prime-number Generation.

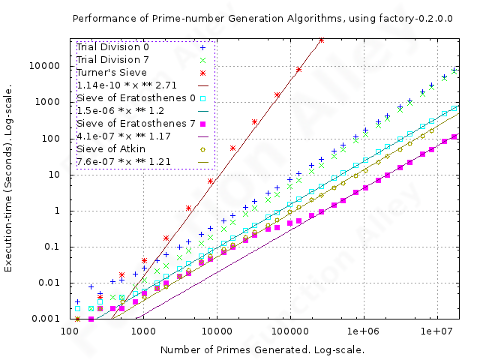
Though a wheel can also be used to pre-sieve candidates before applying Turner's sieve, this actually proved counterproductive; which roughly agrees with the conclusions of Melissa E. O'Neill.
Trial Division, & the Sieve of Eratosthenes, have been plotted for a wheel built from either zero (equivalent to not using a wheel at all) or seven primes.
Because the Sieve of Atkin is bounded, the optimal size for the wheel has been automatically estimated from the length of the required range of primes.

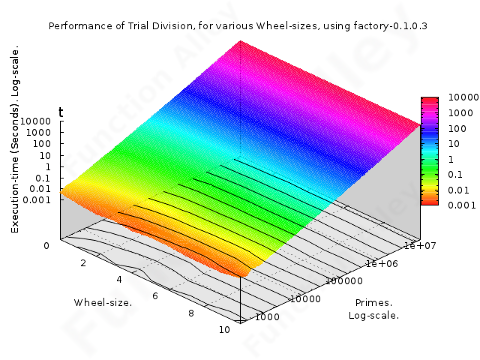
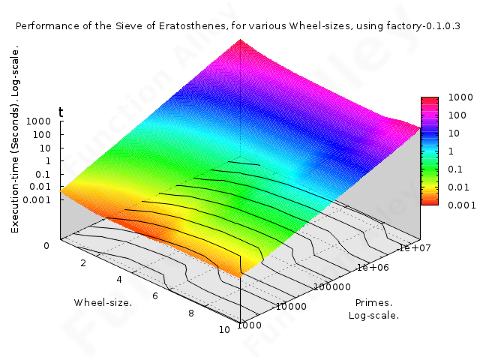
The 3-D plots have contours of constant execution-time, projected onto the base. These contours are separated by a constant time-ratio, rather than a constant absolute difference, in accordance with the logarithmic scale.

Trial Division:

As implemented here, this algorithm has polynomial time-complexity of approximately O(n^1.4). The implementation has been improved by means of a wheel, whose parameterised, but static, size, marginally improves performance. The lazy construction of the wheel ensures that when it is so grossly oversized, that less than one rotation is required to roll the length of the primes demanded, its unused parts aren't even constructed. Contrary to expectations, this lazy construction, also results in little detrimental impact on the time required to find the smaller primes. All attempts to construct a space-saving wheel, leveraging reflection around its axis of symmetry, ruined this beneficial laziness, & were consequently abandoned.

The memory-requirement was linear, & slightly greater for larger wheels. It clearly exhibits some staggering, which may be due to the policy by which the heap is expanded by the ghc-runtime.

Turner's sieve:

Though fascinatingly terse, this algorithm, as implemented here, has a disastrous polynomial time-complexity, of approximately O(n^2.7). Though it's essentially Trial Division, its performance is worse.

Though poor, the memory-consumption is unlikely to be an issue, because the disastrous performance provides a compelling reason to avoid exploring its depths. Because of its non-tail-recursive definition, it exceeded the ghc-runtime's default 8 MiB stack-size, when attempting to find 2¹⁸ primes.

Sieve of Eratosthenes:

This algorithm has a superior, but still polynomial, time-complexity of approximately O(n^1.2). The implementation has been improved by means of a wheel, whose parameterised, but static, size, critically affects performance; though it doesn't improve the time-complexity. The logarithmic scale understates this effect, but it is revealed by the contour-lines inscribed on the base of the 3-D plot. The contours illustrate the diminishing returns from increases to the wheel-size, & an abrupt degradation in the performance, at a wheel-size which depends on the number of primes demanded. Wheels which exceed this optimal size incur a performance-penalty, because the demand for primes doesn't require even one rotation; though, because of its lazy construction, this performance-penalty isn't as bad as the meteoric growth in the circumference of the wheel, with the number of primes represented, might suggest. Quite why the beneficial effect of the wheel is greater than when applied to Trial Division, isn't clear.

As implemented here, the memory-requirement is dominated, by the repository of multiples of those primes already discovered, which grows linearly. The wheel, apparently reduced the memory-requirement.

The Sieve of Atkin:

Though the algorithm has a similar time-complexity to the Sieve of Eratosthenes, it is slower by a constant factor. Profiling reveals that sorting the results from the evaluation of the polynomials is, as predicted, responsible for most of the time required.

The total space-requirement is slightly greater than the Sieve of Eratosthenes, but grows at a similar rate. Profiling reveals that sorting is also responsible for the majority of this.

Conclusions

The space-complexity of all the algorithms tested was linear, & of a slightly lower constant of proportionality when a larger wheel was used.

Trial Division:: Conceptually simple, & simple to implement, but only suitable for the generation of small primes.
Turner's sieve:: Though reducing one's implementation to the bare minimum (golfing), has a strange fascination, this algorithm is little more.
Sieve of Eratosthenes:: The performance exceeded those of the other implementations tested, though some care must be taken in the choice of an appropriate wheel-size. This is annoying, since the unbounded implementation of the core algorithm, requires no access to the maximum prime which will ultimately be demanded; thus one must, as currently implemented, arbitrarily select a wheel-size with broad applicability.
The Sieve of Atkin:: Though the performance is only marginally worse than the Sieve of Eratosthenes, it was considerably more complex to implement, & suffers from the constraint that it is bounded. Though one can automatically estimate the optimal size of the wheel, the theoretical efficiency is ruined by the requirement (as implemented here), to sort a list of integers.